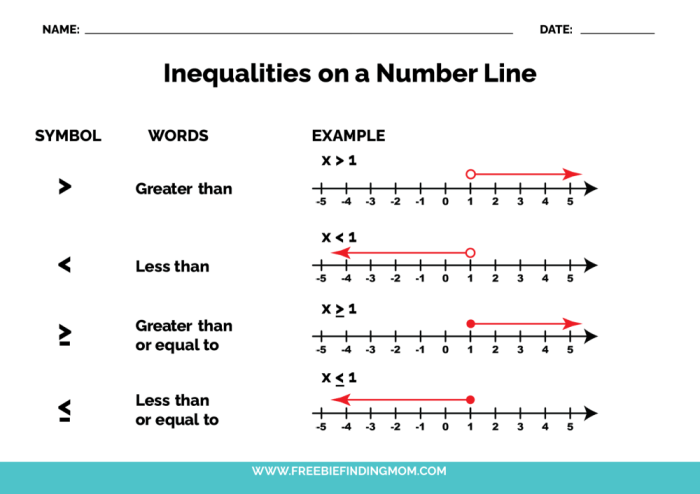
Graph the inequality h 46 – Dive into the fascinating world of inequalities with graph the inequality h ≥ 46. This guide will lead you through a step-by-step exploration of graphing inequalities, identifying solutions, and discovering their practical applications.
From the coordinate plane to real-world scenarios, this article unveils the power of inequalities in mathematics, physics, and economics.
Graphing the Inequality
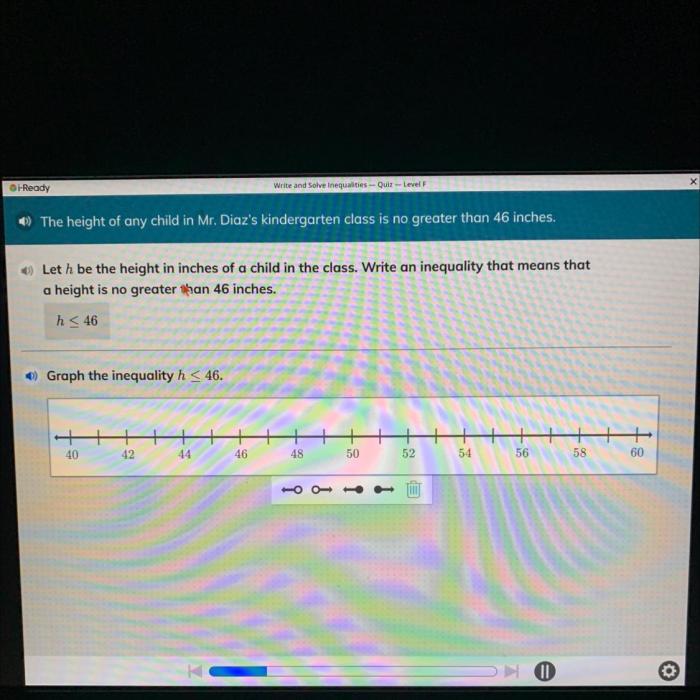
To graph the inequality h ≥ 46, follow these steps:
- Draw the horizontal line y = 46. This line represents the boundary of the inequality.
- Shade the area above the line.The shaded area represents the solutions to the inequality h ≥ 46.
The graph of the inequality should look like this:

Identifying Solutions
In an inequality, a solution is a value that makes the inequality true. For example, in the inequality h ≥ 46, any value of h that is greater than or equal to 46 is a solution.
Examples
Here are some examples of points that satisfy the inequality h ≥ 46:
- h = 46
- h = 47
- h = 50
Here are some examples of points that do not satisfy the inequality h ≥ 46:
- h = 45
- h = 40
- h = 30
Truth Table
The following table lists several points and their corresponding truth values for the inequality h ≥ 46:
| h | h ≥ 46 |
|---|---|
| 46 | True |
| 47 | True |
| 50 | True |
| 45 | False |
| 40 | False |
| 30 | False |
Shading the Solution Region
Once the boundary line has been drawn, the next step is to shade the solution region. This region represents the area on the coordinate plane where the inequality is true.
Graphing the inequality h > 46 can be a bit tricky, but with a little practice, you’ll get the hang of it. If you’re looking for some extra help, check out this Abeka Algebra 2 quiz that covers a variety of topics, including graphing inequalities.
Once you’ve mastered graphing h > 46, you’ll be well on your way to becoming a math whiz!
To determine which side of the boundary line to shade, we need to consider the inequality symbol. If the inequality is less than ( <) or less than or equal to (≤), we shade the region below the line. If the inequality is greater than (>) or greater than or equal to (≥), we shade the region above the line.
Points in and Outside the Solution Region
| Points in the Solution Region | Points Outside the Solution Region |
|---|---|
| (0, 0) | (0, 5) |
(-2,
|
(2, 7) |
(3,
|
(-3, 6) |
Applications of the Inequality: Graph The Inequality H 46
Inequalities have a wide range of applications in various fields, including mathematics, physics, and economics. The inequality h ≥ 46 is particularly useful for solving problems related to height or elevation.
Mathematics
In mathematics, inequalities can be used to:
- Compare the sizes of numbers
- Solve equations and systems of equations
- Model real-world situations
For example, the inequality h ≥ 46 can be used to find the minimum height requirement for a roller coaster.
Physics, Graph the inequality h 46
In physics, inequalities can be used to:
- Describe the motion of objects
- Calculate forces and energies
- Model physical systems
For example, the inequality h ≥ 46 can be used to determine the minimum height from which an object must be dropped to reach a certain velocity.
Economics
In economics, inequalities can be used to:
- Model supply and demand
- Analyze market trends
- Make predictions about economic behavior
For example, the inequality h ≥ 46 can be used to determine the minimum price at which a product must be sold to make a profit.
FAQ
What is the solution region for h ≥ 46?
The solution region is the area above the horizontal line y = 46 on the coordinate plane.
How do you shade the solution region?
Shade the area above the boundary line y = 46.
What are some applications of inequalities in real life?
Inequalities are used in various fields, such as determining the feasibility of solutions in mathematical problems, calculating velocity in physics, and analyzing economic data.